Materialien zum Unterricht
Mittelpunkt und Mittelsenkrechte auf einer Strecke
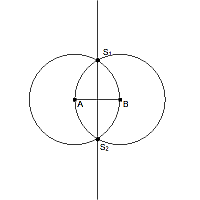
Zur Konstruktion des Mittelpunktes auf einer Strecke werden um die beiden Endpunkte jeweils ein Kreis gezeichnet, der als Radius genau die Streckenlänge hat. Die Verbindung der beiden Schnittpunkte der kreise geht genau durch die Mitte der Strecke.
Die Linie, die die beiden Schnittpunkte der Kreise miteinander verbindet, ist die Mittelsenkrechte auf der Strecke.
Zeichne eine Strecke AB.
|
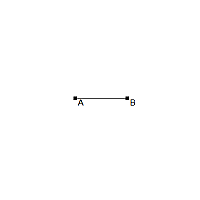 |
| Zeichne um A einen Kreis mit dem Radius AB. | 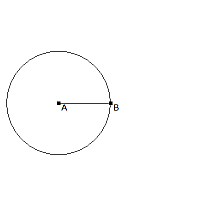 |
| Zeichne um B einen Kreis mit dem Radius BA. | 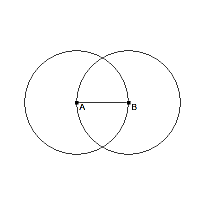 |
Bestimme die Schnittpunkte S1 und S2 der beiden Kreise.
Test: Beim Ziehen am Punkt A oder B müssen die beiden neuen Punkte auch wirklich die Schnittpunkte bleiben. |
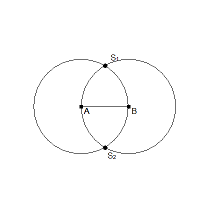 |
Zeichne eine Gerade durch diese beiden Schnittpunkte.
|
 |
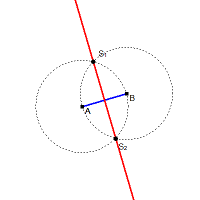
Test: Ziehe am Punkt B. Die Gerade muss weiterhin senkrecht durch die Mitte der Strecke gehen. Gestalte die Konstruktion farbig. Klicke dazu mit der rechten Maustaste auf das Objekt, das verändert werden soll. |
 |
Aufgabe:
|
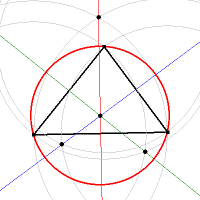 |