Materialien zum Unterricht

Schlüssel

Mit Hilfe der Funktion zum Erstellen einer Primzahl werden nun die Schlüssel erzeugt. Damit das Ganze überschaubar bleibt, arbeitet man mit Primzahlen unter 20.

Der Funktion zum Erstellen einer Primzahl wird der Maximalwert übergeben und die Funktion liefert eine Primzahl zwischen 3 und dem Maximalwert zurück.

Prim-Funktion

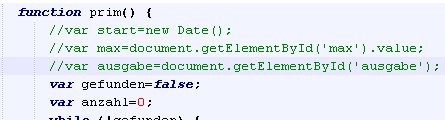
Entferne alles Unnötige aus der Funktion prim(). Weil man aber nicht genau weiß, was wirklich unnötig ist, kommentiert man die vermeintlich überflüssigen Zeilen mit // aus. Damit werden sie nicht interpretiert.
Der Funktion soll der maximale Wert übergeben werden und sie soll die gewürfelte Primzahl zurückgeben.
Die Funktion heißt dann prim(max). max ist eine Variable, in der Funktion verwendet werden kann.
Nach dem Bestimmen der Primzahl wird sie über return zurückgegeben: 
return zahl;

Öffentlicher Schlüssel

Aufgabe: Schreibe eine neue Funktion schluessel(), die folgendes macht:
  1. in zwei Variablen p und q werden zwei Primzahlen zwischen 2 und 20 abgelegt. Die beiden Primzahlen dürfen nicht gleich sein. (Hinweis: Nutze eine kopf- oder fußgesteuerte Schleife und erzeuge solange eine Primzahl q, bis sie nicht mit p übereinstimmt.
  2. Berechne daraus den RSA-Modul: N=p•q
  3. Berechne die Eulersche Funktion phi von N:
    phi=(p-1)•(q-1)
  4. Wähle eine zu phi teilerfremde Zahl größer als 1. Die Zahl heißt e.
    Dazu kann man alle Zahlen von 2 aufwärts zählen und jeweils prüfen, ob sie zu phi teilerfremd ist. Teilerfremd ist sie dann, wenn die Modulo-Funktion einen Wert ungleich 0 liefert.
    Beispiel: Wenn phi=72, dann ist 5 die erste Zahl, durch die 72 nicht teilbar ist.
  5. Alle Werte sollen nach Drücken eines Knopfen bestimmt und angezeigt werden.
Die Werte e und N sind der öffentliche Schlüssel. Damit kann Verschlüsselt werden.

Wählt man einen größeren Maximalwert, dauert es zwar etwas länger, aber die Zahlen werden auch größer:

Hinweis: JavaScript rechnet nur mit Zahlen bis zu 17 Stellen. Bei größeren Zahlen werden die letzten Stellen mit Nullen aufgefüllt.

Privater Schlüssel

Zum Entschlüsseln ist der private Schlüssel zu erzeugen. Für den privaten Schlüssel d gilt:

e · d ≡ 1 (mod phi(N))

e mal d und 1 sind kongruent modulo phi(N)

Das bedeutet: Multipliziert man e und d miteinander und teilt das Produkt durch phi(N), so muss als Rest 1 übrig bleiben.

Dazu wird eine for-Schleife geschrieben, die eine Zählvariable i von 1 an nach oben zählt. Der zweite Teil in der Klammer der for-Schleife stellt die Bedingung für die Fortsetzung der Schleife dar. Die Schleife wird dann fortgesetzt, wenn diese Bedingung erfüllt ist.

Eine Anweisung braucht die Schleife nicht durchzuführen. Der übliche folgende Block in den geschweiften Klammern kann weggelassen werden.

Bedingungen für das Fortsetzen der Schleife:

  1. Die Zählvariable ist kleiner als phi. Falls i größer als phi wird, lässt sich kein d finden.
    UND
  2. das Produkt aus e und i modulo phi ist ungleich 1. Wenn diese Operation 1 ergibt, ist der private Schlüssel gefunden.

Realisiere zuerst nur die 1. Bedingung. Damit wird die Schleife immer abgebrochen. Die zweite Bedingung wird über && zur ersten Bedingung hinzugefügt.

Die Probeausgabe muss immer 1 liefern.

d ist der private Schlüssel, der zum Entschlüsseln benötigt wird.

Achtung: Falls die Schleife wegen der Gleichheit von i und phi abgebrochen wurde, muss das durch ein Alert-Fenster signalisiert werden. Dann ist mit den bestimmten Zahlen keine Verschlüsslung möglich.

zurück