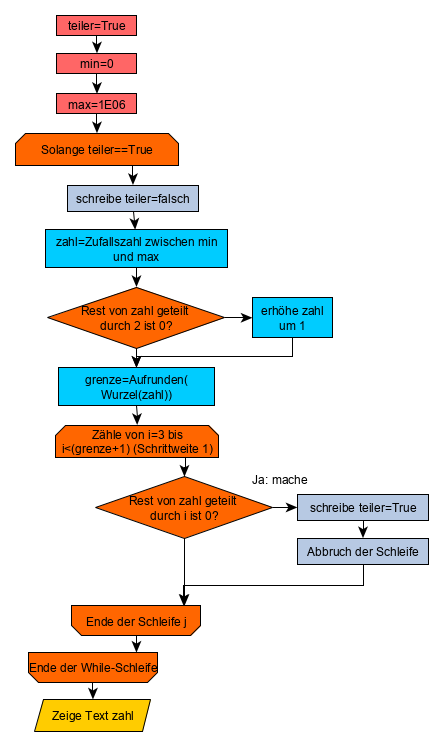
Bisher gibt es noch keine Möglichkeit, mit Hilfe einer Rechenvorschrift eine Primzahl einfach so zu bestimmen. Braucht man eine zufällige Primzahl zwischen 2 und einer Obergrenze, muss man eine zufällige Zahl bestimmen und dann testen, ob es eine Primzahl ist. Fällt der Test negativ aus, muss man eine neue Zufallszahl bestimmen und den Test erneut ausführen.

Prinzip: Eine Primzahl ist eine Zahl größer als 1, die nur durch 1 und sich selber teilbar ist. Es muss also nur geprüft werden, ob ein Primzahlenkandidat durch eine Zahl ohne Rest teilbar ist. Wenn das der Fall ist, ist er durchgefallen :-(.

Als erstes testet man auf 2 als Teiler. Liefert die Modulo-Funktion eine 0 (also durch 2 geteilt und keinen Rest), ist die Zahl gerade. Dann wird einfach 1 addiert und die Zahl ist ungerade. Damit fällt im folgenden Test die 2 als Teiler raus und es kann mit der 3 begonnen werden.

Wie weit muss man testen? Es soll am Beispiel der 18 gezeigt werden. Es wird immer 18 durch den Teiler geteilt und das ganzzahlige Ergebnis sowie der Rest der ganzzahligen Division betrachtet. Wem das Verfahren irgendwie bekann vorkommt, erinnert sich sicher gerade an die ersten Teilerübungen in der Grundschule.

Teiler	Ergebnis	Rest
3	6	0
4	4	2
5	3	3
6	3	0
7	2	4
8	2	2
9	2	0
10	1	8
11	1	7

Ab der 10 geht es immer so weiter. Das Ergebnis ist 1 und der Rest nähert sich der 18.
Das heißt aber, dass man eigentlich nur die 3, die 4 und die 5 prüfen muss. Denn die 6 kann wegfallen, da bei der Division durch 6 die 3 ohne Rest das Ergebnis ist. Die 3 ist aber schon geprüft worden.

• Der Primzahlentest muss nur bist zur aufgerundeten Wurzel aus der Testzahl gemacht werden.
• Liefert eine Modulo-Funktion als Ergebnis 0, kann Zählschleife abgebrochen werden.