Materialien zum Unterricht
RSA-Verschlüsslung
1. Schritt: Zwei Primzahlen p und q werden über jeweils einen Funktionsaufruf bestimmt.
Das Suchen einer Primzahl wird in eine Funktion gepackt. Die Funktion wird mit der Übergabe der oberen Grenze aufgerufen und liefert über return(zahl) die gefundene Primzahl zurück.
Der Aufruf erfolgt dann z.B. über
p=primzahl(1000)

2. Schritt: Werte ausgeben.
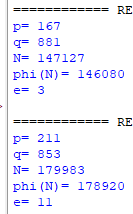
Zur Kontrolle werden während des Programms alle errechneten Werte ausgegeben. Den Anfang machen die beiden Primzahlen.

3. Schritt: N und phi(N) werden berechnet
N ist einfach das Produkt aus den beiden Primzahlen. phi(N) ist die eulersche Phi-Funktion: phi(N)=(p-1)·(q-1). Diese Zahl wird gleich wieder benötigt.

4. Schritt: eine teilerfremde Zahl e zu phi(N) wird ermittelt
Wähle eine zu phi(N) teilerfremde Zahl größer als 1. Die Zahl heißt e.
Dazu kann man in einer while-Schleife alle Zahlen von 2 aufwärts zählen und jeweils prüfen, ob sie zu phi(N) teilerfremd ist. Teilerfremd ist sie dann, wenn die Modulo-Funktion einen Wert ungleich 0 liefert.
Beispiel: Wenn phi=72, dann ist 5 die erste Zahl, durch die 72 nicht teilbar ist.
Die beiden Werte N und e bilden den öffentlichen Schlüssel. Sie müssen an die Stellen gegeben werden, die eine verschlüsselte Nachricht an mich schicken möchten.
5. Schritt: Der private Schlüssel d wird berechnet
Zum Entschlüsseln ist der private Schlüssel zu erzeugen. Für den privaten Schlüssel d gilt:
e · d ≡ 1 (mod phi(N))
e mal d und 1 sind kongruent modulo phi(N)
Das bedeutet: Multipliziert man e und d miteinander und teilt das Produkt durch phi(N), so muss als Rest 1 übrig bleiben.
Dazu wird eine while-Schleife geschrieben, die eine Variable d von 1 an nach oben zählt.
Bedingungen für das Fortsetzen der Schleife:
- Die Variable d ist kleiner als phi(N). Falls d genau so groß wie phi(N) wird, lässt sich kein d finden.
UND - das Produkt aus e und d modulo phi(N) ist ungleich 1. Wenn diese Operation 1 ergibt, ist der private Schlüssel gefunden.
Realisiere zuerst nur die 1. Bedingung. Damit wird die Schleife immer abgebrochen und d ist so groß wie phi(N). Die zweite Bedingung wird über & zur ersten Bedingung hinzugefügt:
((erster Vergleich) & (zweiter Vergleich)) oder
((erster Vergleich) and (zweiter Vergleich))

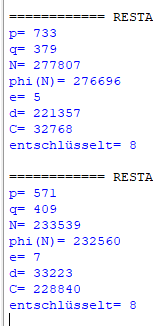
So sollte die Ausgabe dann aussehen.:

6. Schritt: Mit dem öffentlichen Schlüssel wird eine Zahl verschlüsselt
Zu Beginn soll einfach eine Ziffer verschlüsselt werden. Wähle eine kleine Ziffer, z.B. 8.
Die Verschlüsslungsfunktion hat die Form:
C ≡ Ke mod N
Das heißt: der Klartext K (also z.B. die 8) wird hoch e genommen. Diese Zahl wird modulo N gerechnet. Der dann verbleibende Rest ist der Geheimtext C. Wichtig: K muss kleiner als N sein.
7. Schritt: Mit dem privaten Schlüssel wird eine Zahl entschlüsselt
Die Entschlüsslungsfunktion hat die Form:
K ≡ Cdmod N
Wenn alles funktioniert, erscheint am Ende des Programms in der Ausgabe die Zahl, die Verschlüsselt wurde.